ACP-CM2
Cliquez sur les titres pour accéder aux contenus des onglets
- Présentation
- Type de problèmes
- Organisation des ACP
- Déroulement des ACP
- ACP en vidéo
- Bibliothèque des ACP en CM2
L’enseignant est invité à partager sa classe en au moins deux groupes :
- un groupe d’élèves en ACP dont il guidera les réflexions
- un groupe d’élèves qui fonctionnent en autonomie autour des AEI.
Les ateliers ACP fonctionnent avec un petit groupe d’élèves afin que tous et chacun puissent s’approprier, se représenter et modéliser ces situations avant de les résoudre. La démarche s’appuie sur les représentations des élèves en fonction du type de problème.
Le but principal est de favoriser la prise de paroles des élèves et la mise en place de débats (ce qui nécessite un nombre peu élevé d’élèves). Ce fonctionnement met en valeur le rôle pédagogique de l’erreur, de la « recherche » en petits groupes, de la justification verbale des « propositions des groupes », et le rôle de l’enseignant en « conducteur des débats » et du déplacement didactique de celui-ci : ce n’est pas lui qui donne la solution mais c’est lui qui permet aux élèves de défendre leur solution, de l’argumenter et d’aboutir à un consensus des différents groupes.
En CM2, la démarche s’appuie sur les représentations des élèves en fonction du type de problème.
Trois types de problèmes sont plus particulièrement explorés dans les ACP :
Des problèmes de type I pour apprendre à :
- Tirer des informations de différents supports : image, texte, schéma, tableau, graphique…
- Traduire des informations d’un support à un autre
- Organiser et traiter logiquement les informations
Pour avoir plus d'informations, cliquez sur la flèche verte à droite
Les problèmes de type I visent à travailler plus spécifiquement la prise d’informations dans les énoncés. Ceux-ci peuvent être donnés sous différentes formes : un texte, un tableau, un graphique, un schéma... Dans un même problème, plusieurs formes peuvent être présentes.
Les ACP de type I permettent aux élèves de prendre conscience que :
- Les informations ne sont pas toujours données par un énoncé sous forme de texte et peuvent être dispersées à plusieurs endroits d’un document.
- La lecture et l’interprétation de ces informations données sur les différents supports aident à l’élaboration d’hypothèses sur le sens des énoncés. Le travail en groupe restreint favorise les possibilités d’exprimer précisément ces hypothèses, de les confronter et de les mettre en débat afin d’être comprises au plus près de leur signification.
La démarche pédagogique utilisée dans les ACP de type I :
Il s’agit principalement d’un travail de mise en relation entre les divers registres. Des énoncés sont présentés aux élèves sous différentes formes et leur tâche consiste à identifier ceux qui sont identiques. Par exemple, parmi plusieurs problèmes écrits en langage courant, les élèves doivent retrouver pour chacun d’entre eux, un tableau qui les représente. De même, ils peuvent avoir à associer des textes et des graphiques, des textes et des schémas, des schémas et des calculs…
Dans ce cas-là, la résolution des problèmes n’est qu’un objectif second.
Des problèmes de type II pour apprendre à :
- Reconnaitre les différentes structures additives des problèmes arithmétiques
- Reconnaitre les différentes structures multiplicatives des problèmes arithmétiques
Pour avoir plus d'informations, cliquez sur la flèche verte à droite
Les problèmes de type II cherchent à développer des stratégies de résolution de problèmes par une modélisation logique basée sur la typologie de G. Vergnaud. Résoudre un problème c’est être capable d’identifier la classe de problèmes auquel il appartient. Bien souvent, l’enfant se réfère aux quatre classes des opérations arithmétiques les plus expertes qui donnent la solution. Il identifie donc quatre catégories de problèmes : ceux qu’on résout avec une addition, ceux qui se résolvent à l’aide d’une soustraction, ceux dont la solution est trouvée avec une multiplication ou ceux résolus par une division.
Cette classification n’est pas pertinente car elle ne correspond pas aux différentes structures conceptuelles c’est-à-dire aux différents types de relations entre les données. Par exemple, parmi les structures dites additives, certaines de ces relations sont semblables et renvoient soit à une addition soit à une soustraction, alors que d’autres diffèrent tout en étant traduites mathématiquement par la même opération mathématique.
Ainsi, deux situations d’accroissement peuvent se résoudre à l’aide d’une addition si on cherche l’état final ou par une soustraction si on cherche l’état initial.
|
Structure arithmétique du problème |
Problème |
Relation entre les données |
Solution |
||||||
|
Accroissement 1 |
Au début d’une partie d’un jeu Maya possédait 4 jetons dans sa boite. Au cours de la partie elle en gagne 5. Combien de jetons a-t-elle à la fin de la partie ?
|
|
4+5 |
||||||
|
Accroissement 2 |
Au début d’une partie d’un jeu Maya possédait des jetons. Au cours de la partie elle en gagne 5. A la fin de la partie elle a 9 jetons dans sa boite . Combien de jetons avait-t-elle au début de la partie ? |
|
9-5 |
Par contre, une situation d’accroissement ou une situation de comparaison ou encore une situation de réunion de deux parties diffèrent par les liens sémantiques qui existent entre les données mais se traduisent toutes mathématiquement par une addition.
|
Structure arithmétique du problème |
Problème |
Relation entre les données |
Solution |
||||||
|
Un accroissement |
Au début d’une partie d’un jeu Maya possédait 4 jetons dans sa boite. Au cours de la partie elle en gagne 5. Combien de jetons a-t-elle à la fin de la partie ? |
|
4+5 |
||||||
|
Une comparaison |
Lola a 4 ans. Son frère a 5 ans de plus que Lola . Quel âge a son frère ?
|
|
4+5 |
||||||
|
Une réunion de deux parties |
Nora possède 4 billes bleues et 5 billes rouges. Combien Nora possède-t-elle de billes en tout ?
|
|
4+5 |
||||||
De même au sein des structures dites multiplicatives, des situations de proportionnalité simples peuvent se résoudre soit par une multiplication soit par une division.
|
Structure arithmétique du problème |
Problème |
Relation entre les données |
Solution |
||||||
|
Proportionnalité 1 |
Dans une classe, on répartit les élèves en 4 équipes de 6 élèves. Combien y a-t-il d’élèves dans la classe ?
|
Recherche du produit total
|
6 x 4 |
||||||
|
Proportionnalité 2 |
Dans une classe de 24 élèves, on répartit les élèves en équipes de 6 élèves. Combien obtient-on d’équipes ?
|
recherche du nombre de parts
|
24 : 6 Division quotition |
||||||
|
Proportionnalité 3 |
Dans une classe de 24 élèves, on répartit les élèves en 4 équipes. Combien y a-t-il d’élèves par équipe ?
|
recherche de la valeur d’une part
|
24 : 4 Division partition |
Tandis que des situations qui mettent en relation les données de façon différente, par exemple des comparaisons et des proportionnalités simples, se traduisent par une même multiplication.
|
Structure arithmétique du problème |
Problème |
Relation entre les données |
Solution |
||||||
|
Une comparaison |
Dans une classe, il y a 4 garçons. Il y a 6 fois plus de filles que de garçons. Combien y a-t-il de filles ?
|
Relation ternaire
|
6 x 4 |
||||||
|
Une proportionnalité |
Dans une classe, on répartit les élèves en 4 équipes de 6 élèves. Combien y a-t-il d’élèves dans la classe ?
|
Relation quaternaire
|
6 x 4 |
||||||
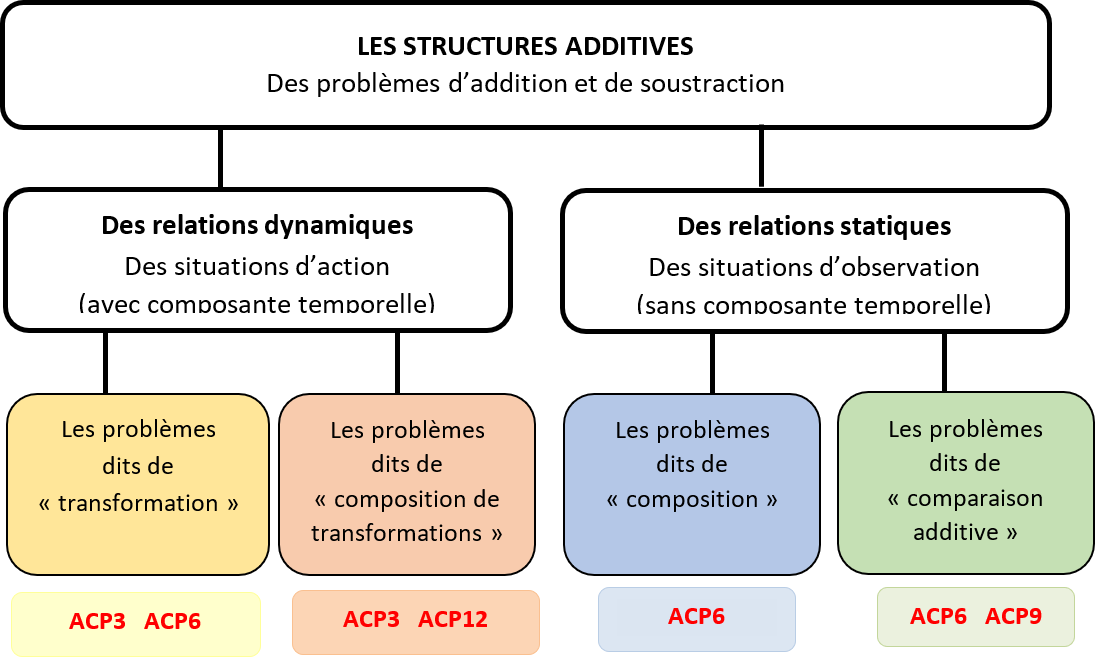
Les différentes structures additives étudiées dans les ACP :
- Les situations de transformations positives (accroissements) et négatives (diminutions) : on recherche soit le nombre final, soit le nombre de la transformation, soit le nombre initial.
- Les situations de réunions de deux parties en un tout avec la recherche soit du tout d’une partie
- Les situations de comparaisons additives positives (de plus) ou négatives (de moins) : on recherche soit l’une des deux quantités comparées, soit l’écart entre les deux.
- Les situations de compositions de transformations : par exemple, deux transformations qui se suivent, toutes deux positives ou toutes deux négatives, ou une positive et une négative.
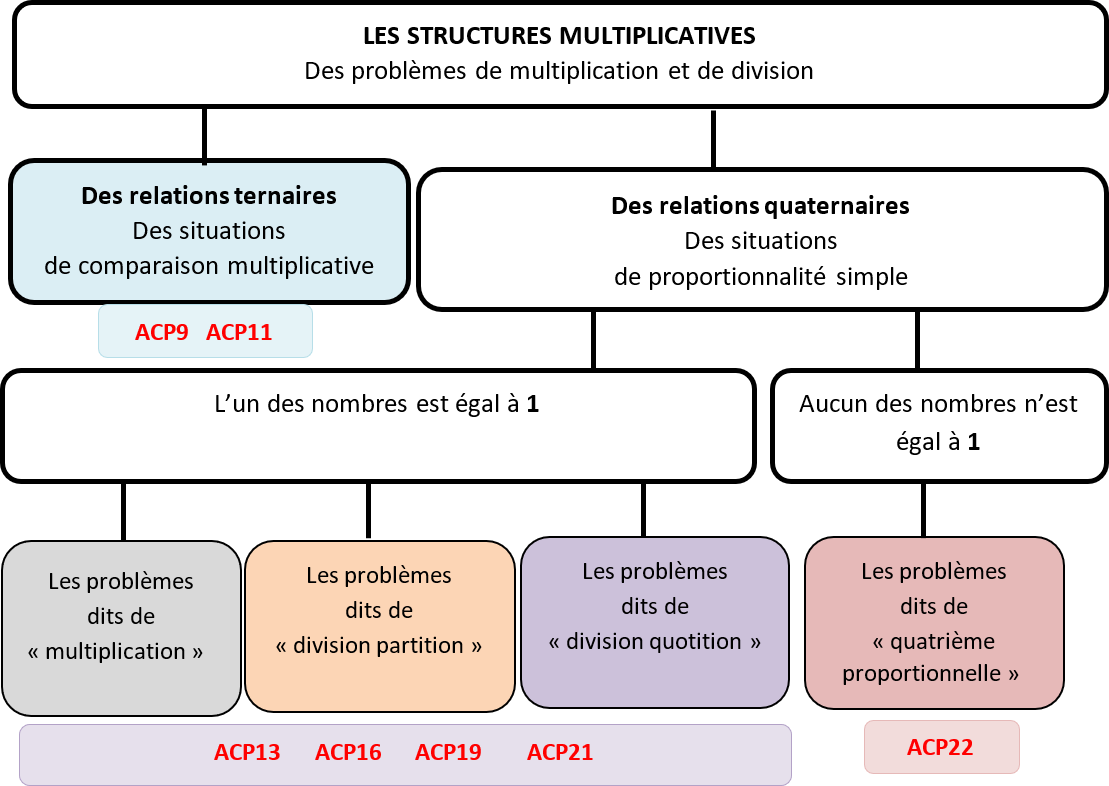
Les différentes structures multiplicatives étudiées dans les ACP
- Les situations de comparaisons multiplicatives positives (fois plus) et négatives (fois moins) : on recherche soit l’une des deux quantités comparées, soit le rapport entre les deux.
- Les situations de proportionnalité simple : soit on recherche le produit total, soit le nombre de parts, soit la valeur d’une part, soit encore le rapport de proportionnalité, en s’appuyant sur la valeur unitaire ou non.
Ces différentes structures sont étudiées dans les ACP de ROMA selon une progression rigoureuse proposée depuis le CP jusqu’à la fin du cycle 3.
La démarche pédagogique utilisée dans les ACP de type II :
- De façon progressive au cours d’une année ou sur les cycles 2 et 3, un premier travail s’articulera autour de l’identification des structures pour favoriser la généralisation des relations entre les informations d’un problème. C’est ainsi que les élèves sont régulièrement confrontés à un ensemble de 6 à 8 énoncés de problèmes : la tâche demandée est de se centrer sur la structure elle-même des problèmes pour effectuer un classement de ces problèmes au niveau des signifiés sans prendre en compte des classements liés aux signifiants ou aux opérations mathématiques.
- Puis, au sein de chaque structure, un travail de modélisation et de schématisation permettra de mobiliser des procédures de résolution adaptées.
- Enfin, dans tous les ACP, un soin particulier est pris pour favoriser l'explicitation des stratégies de résolution. L'élève doit être amené à justifier ses choix, à expliciter sa démarche. Cette démarche vise à apprendre, petit à petit, à formaliser des raisonnements de plus en plus complexes.
Elaborer des similitudes entre les différents problèmes permet aux élèves d’accéder au modèle mathématique sous-jacent. La généralisation de ces modèles sous forme de catégories de problèmes de référence favorise alors le transfert par analogie de chaque structure reconnue à des problèmes nouveaux ainsi que les stratégies de résolution liées à chacune.
Des problèmes de type III pour apprendre à :
- Gérer simultanément la prise d’informations et leur traitement dans des tâches complexes
- Organiser un raisonnement à plusieurs étapes
Pour avoir plus d'informations, cliquez sur la flèche verte à droite
Les problèmes de type III
Le travail effectué dans les ACP de type I autour de la prise des informations et celui effectué dans les ACP de type II autour de la mise en relation sémantique des informations, se trouvent réinvestis et finalisés dans les tâches de résolution des situations de type III. Les problèmes de type III visent à la fois à savoir extraire et trier les informations de différents supports et à savoir les traiter en utilisant les modèles élaborés dans la reconnaissance des différentes structures de problèmes arithmétiques. Dans ROMA, une attention particulière est portée à relier les mathématiques à la vie « réelle » en proposant des situations ancrées dans la vie quotidienne ou en rapport avec les autres disciplines scolaires.
D’un point de vue pédagogique, ce type d’activité s’apparente à une tâche complexe, c’est-à-dire une tâche dont la résolution amène l’élève à utiliser, en les articulant, des ressources internes (culture, capacités, connaissances, etc.) et externes (documents, aides méthodologiques, protocoles, notices, etc. ).
Les compétences travaillées
Etre capable de :
1. prendre des informations dans différents supports (image, texte, schéma, tableau, graphique…)
2. traduire des informations d’un support à un autre (changement de registre)
3. reconnaitre les différentes structures additives des problèmes arithmétiques
4. reconnaitre les différentes structures multiplicatives des problèmes arithmétiques
5. organiser et traiter logiquement les informations
6. résoudre un problème en gérant simultanément la prise d’informations et leur traitement
7. organiser un raisonnement à plusieurs étapes
8. justifier et communiquer une résolution
Les séances
Il est prévu 1 séance d’atelier par semaine et par élève, soit 2 séances pour le professeur par semaine en demi-classe. L’enseignant peut trouver pour chaque atelier des fiches * ou des fiches ** qui lui permettront de différencier son travail et créer des groupes de besoin si nécessaire.
Les ateliers d’ACP sont prévus pour être organisés en parallèle des activités d’entrainement en maths sur le programme avec les AEI.
Cliquez sur le titre ci-dessous pour avoir un exemple d’organisation de la classe.
|
Classe partagée par l’enseignant en deux ½ Groupes |
||
|
Groupe ACP |
Groupe en AEI |
|
1ere semaine |
ACP de type I Prendre et déduire des informations d’un tableau |
Travail en autonomie sur la compétence NE1 de tous les élèves
|
2e semaine |
ACP de type II Etudier et schématiser les transformations additives |
Travail en autonomie sur la compétence NE2 de tous les élèves
|
3e semaine |
ACP de type III L’espace des sciences de Rennes |
Travail en autonomie sur la compétence M1 de tous les élèves
|
4e semaine |
ACP de type I Déductions logiques : les monstres |
Travail en autonomie sur la compétence C1 de tous les élèves
|
5e semaine |
ACP de type II Distinguer les principales structures additives |
Travail en autonomie sur la compétence NE3 de tous les élèves
|
6e semaine |
ACP6 de type III Le catalogue de bricolage |
Travail en autonomie sur la compétence G1 de tous les élèves
|
|
Et ainsi de suite... |
||
Nous proposons de travailler les ACP en suivant une progression qui nous semble particulièrement utile pour les problèmes de type II. De même, nous conseillons d’alterner les problèmes de type I, type II et type III. Les numéros des ACP indiquent cet ordre possible.
Cliquez sur les flèches à droite pour en savoir plus.
ACP1 - faire des inférences (type I)
ACP2 - prendre et déduire des informations d'un tableau (type I)
ACP3 - etudier et schématiser les transformations additives (type II)
ACP4 - l'espace des sciences de Rennes (type III)
ACP5 - déduction logique-les monstres (type I)
ACP6 - distinguer les principales structures additives (type II)
ACP7 - le catalogue de bricolage (type III)
ACP8 - associer énoncés et calculs (type I)
ACP9 - différencier les comparaisons additives et multiplicatives (type II)
ACP10 - les horaires d'avions (type III)
ACP11 - étudier et schématiser les comparaisons multiplicatives (type II)
ACP12 - représenter un problème par un schéma linéaire (type I)
ACP13 - identifier les problèmes multiplicatifs de proportionnalité simple (type II)
ACP14 - représenter un problème par un graphique en bâtons (type I)
ACP15 - les articles de sport (type III)
ACP16 - représenter un problème de proportionnalité par un tableau (type II)
ACP17 - représenter un problème par un diagramme circulaire (type I)
ACP18 - les fournitures scolaires (type III)
ACP19 - proportionnalité-utiliser les rapports entre lignes ou colonnes dans les tableaux (type II)
ACP20 - organiser les données d’un problème dans un tableau (type I)
ACP21 - proportionnalité-utiliser les rapports inverses dans les tableaux (type II)
ACP22 - proportionnalité-les recettes de cuisine (type III)
|
Problèmes de Type I |
Problèmes de Type II |
Problèmes de Type III |
|
ACP1 - faire des inférences |
ACP3 - étudier et schématiser les transformations additives |
ACP4 -l'espace des sciences de Rennes |
|
ACP2 -prendre et déduire des informations d'un tableau ou d’un dessin |
ACP6 - distinguer les principales structures additives |
ACP7 -le catalogue de bricolage |
|
ACP5 -déduction logique-les monstres |
ACP9 –différencier les comparaisons additives et multiplicatives |
ACP10 - les horaires d'avions |
|
ACP8 - associer énoncés et calculs |
ACP11 - étudier et schématiser les comparaisons multiplicatives |
ACP15- les articles de sport |
|
ACP12 -représenter un problème par un schéma linéaire |
ACP13 -identifier les problèmes multiplicatifs de proportionnalité simple |
ACP18 - les fournitures scolaires
|
|
ACP14 -représenter un problème par un graphique en bâtons |
ACP16 -représenter un problème de proportionnalité par un tableau |
ACP22 -proportionnalité-les recettes de cuisine |
|
ACP17 -représenter un problème par un diagramme circulaire |
ACP19 - proportionnalité simple-utiliser les rapports entre lignes ou colonnes dans les tableaux |
|
|
ACP20 -organiser les données d’un problème dans un tableau |
ACP21 - proportionnalité simple-utiliser les rapports inverses dans les tableaux |
La conception d’une séance d’atelier de compréhension de problème
Télécharger la version PDF du diaporama
Vous pourrez aussi voir séparément les différentes phases d'un ACP dans la rubrique "ACP en vidéo"
(Cliquez sur les images pour accéder aux vidéos)
ACP de type 1 : Trier et organiser des informations
|
||||||
|
|
||||||
ACP de type 2 : Différencier les comparaisons additives et multiplicatives
|
||||||
Gestion des interactions dans un ACP
Cliquez sur l'image pour accéder à la vidéo