ACP-CP
Cliquez sur les titres pour accéder aux contenus des onglets
- Présentation
- Place de la manipulation
- Place des activités numériques
- Place des activités langagières
- Organisation
- Bibliothèque
La place de la manipulation dans les ACP de CP
Pourquoi manipuler en résolution de problèmes ?
La manipulation avec un matériel spécifique aide les élèves à illustrer les concepts, à établir des liens et à mieux comprendre les structures des problèmes étudiés. Nous avons élaboré un matériel qui permet aux élèves d’expérimenter et d’utiliser des situations de référence pour chacune des structures des problèmes arithmétiques du CP.
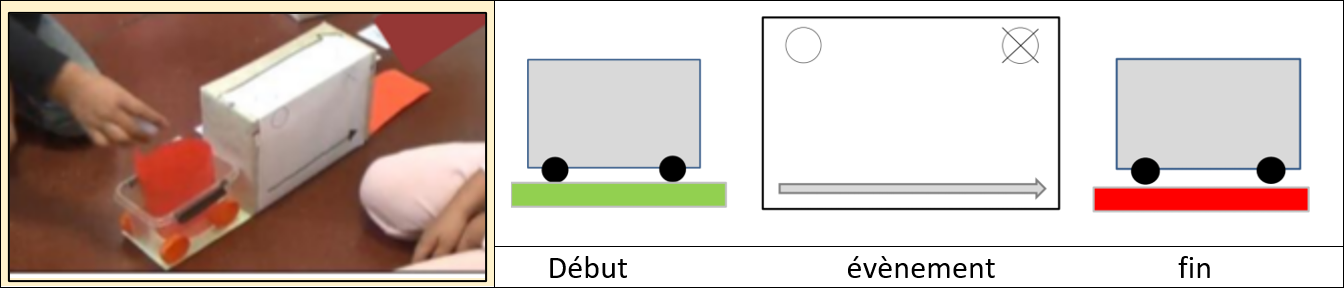
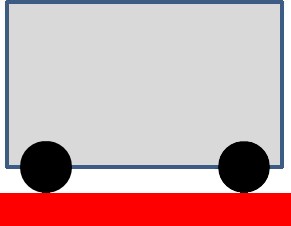
Pour les problèmes de transformation |
|
Les élèves doivent s’approprier les 3 éléments caractéristiques d’une transformation additive. C’est une situation dynamique où une quantité initiale va augmenter ou diminuer au cours du temps (l’événement) et se transformer en une autre quantité (plus ou moins grande) : l’habillage de cette structure sera concrétisé par un camion qui passe dans un garage où a lieu la transformation : un ajout ou un retrait de jetons.
|
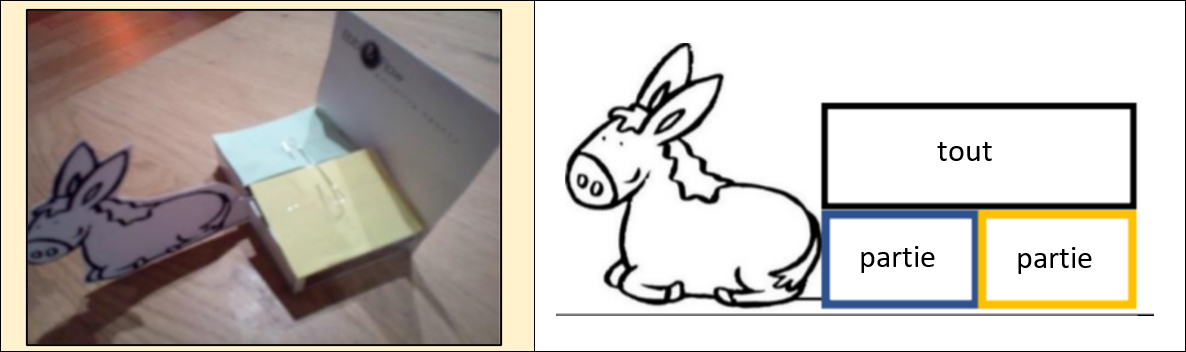
Pour les problèmes de composition |
|
Les élèves doivent s’approprier les 3 éléments caractéristiques d’une composition additive. C’est une situation statique où les éléments « parties » et « tout » sont reliés simultanément, sans déroulement dans le temps : l’habillage de cette structure sera concrétisé par un âne qui transporte des marchandises (jetons) dans ses deux paniers (un bleu et un jaune pour pouvoir les distinguer dans l’énonciation).
|
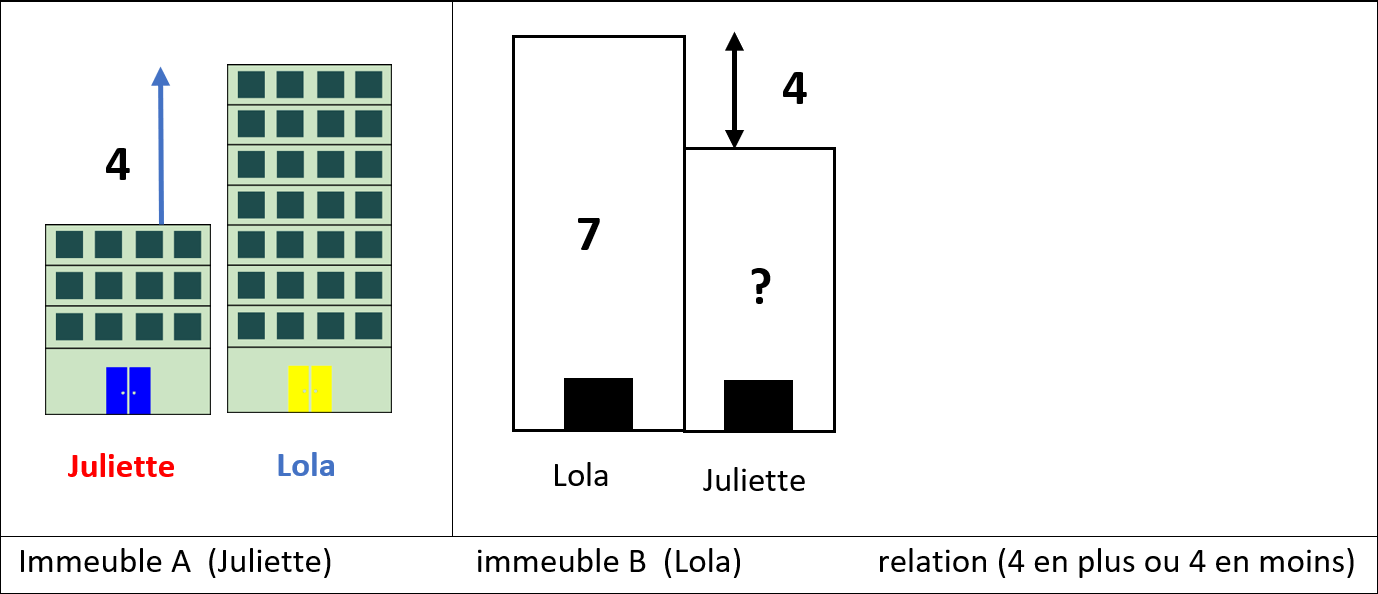
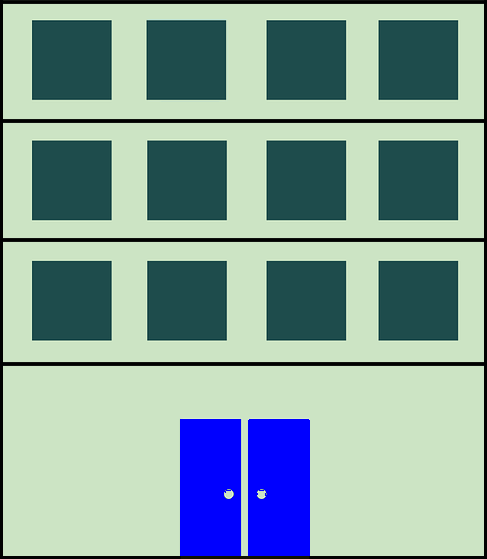
Pour les problèmes de comparaison |
|
Les élèves doivent s’approprier les 3 éléments caractéristiques d’une composition additive. C’est une situation statique où il y a deux états distincts reliés par une comparaison de type « en plus » ou « en moins » : l’habillage de cette structure sera concrétisé par 2 immeubles dont les bases sont alignées et dont on compare le nombre d’étages.
|
Pour les problèmes de partages et de groupements |
|
Les élèves doivent s’approprier les caractéristiques d’une situation multiplicative : cette structure est concrétisée par des coffres à trésors (pierres précieuses ou autres collections) et des pirates qui vont se partager ou grouper leurs trésors.
|
La manipulation de ces divers matériels permet aux élèves :
- De construire une représentation concrète de la situation pour mieux se l’approprier.
- De fabriquer des situations de référence pour retrouver la structure de nouveaux problèmes par analogie : pour chaque type de structure, les élèves ont à disposition le matériel correspondant.
- De soutenir leur activité intellectuelle : pendant la manipulation des supports matériels, les élèves analysent, cherchent, se posent des questions et échangent avec leurs pairs à propos de leur façon de procéder.
- De représenter visuellement leur raisonnement, de mettre plus facilement leur raisonnement à l’épreuve, de l’objectiver et de le confirmer en le communiquant à d’autres.
- De disposer d’un support concret avant de passer à une représentation dessinée, puis schématique et enfin mathématique : en CP, c’est une étape indispensable dans le processus d’abstraction que constitue la modélisation en mathématiques.
De façon générale, la manipulation permet aux enseignants :
- De mettre en place une certaine différenciation pédagogique.
- De leur fournir un terrain d’observation et une base pour saisir et évaluer la compréhension qu’a chaque élève de la situation.
Comment mettre en œuvre cette manipulation ?
Pour chaque module, un premier temps est consacré à la découverte du matériel spécifique proposé. Il est indispensable de laisser aux élèves le temps de s’approprier ce matériel.
Ensuite tout au long des ACP que ce soit en activité individuelle ou par groupes de 2 ou 3 élèves, il est prévu à chaque fois un temps de manipulation qui est souvent accompagné d’activités de description de la manipulation et de la situation étudiée par une phrase, un dessin, un schéma et au final une écriture mathématique.
Certains élèves se détachent spontanément du matériel mais l’enseignant doit être très attentif à ce que les élèves gardent le matériel suffisamment longtemps. Il doit être souple avec l’utilisation du matériel, inciter les élèves à le reprendre à tout moment si des obstacles apparaissent. L’évolution va être différente d’un élève à l’autre. C’est pourquoi, dans tous les ACP, il y a systématiquement des adaptations possibles avec des activités différenciées selon les difficultés ou les performances des élèves.
Pour permettre un temps de stabilisation et de fixation des acquis de chaque atelier, une banque de situations semblables à l’ACP récemment vécu est toujours proposée aux enseignants.
Cependant, on se rend compte au fur et à mesure de l’étude de nouvelles structures que ce qui semblait précédemment acquis se révèle fragile et que la manipulation du matériel doit souvent être reprise. Par exemple quand dans le module 3, les élèves se retrouvent devant la situation de décider si tel problème est un problème de transformation ou de composition, la reprise du matériel et de sa manipulation est bien souvent décisive.
On peut abandonner le matériel qui peut être évoqué par un dessin ou … un schéma mais bien se garder d’aller trop vite vers l’abstraction…
La place des activités numériques dans les ACP de CP
Même en début de CP, les élèves ont déjà une idée préconçue des problèmes : pour eux, à un problème posé, même quand il s’agit d’un atelier de compréhension de problèmes, correspond obligatoirement une réponse « chiffrée », la SOLUTION.
Notre objectif est de lutter contre cette mauvaise habitude du nombre « souverain » :
- On met l’accent sur les structures des problèmes sous-jacentes. On fait classer, comparer, associer des problèmes « qui vont ensemble ». Dans ce type d’activités les nombres en jeu sont souvent les mêmes et les élèves ne peuvent pas se « raccrocher » aux nombres eux-mêmes pour faire leur classement : ils sont « contraints » de s’appuyer sur les structures.
- On demande très peu souvent d’aller jusqu’au bout de la résolution du problème.
- Et enfin on n’utilise jamais de compétences numériques d’un niveau au-delà de ce que les élèves maîtrisent déjà. Donc trouver le nombre-solution n’est plus un enjeu… Au-delà de la compréhension des événements qui constituent l’histoire du problème, il est nécessaire de relier les données entre elles en fonction de la structure sous-jacente du problème. Le but de notre intervention est de faire comprendre qu’il existe une relation entre les nombres plutôt que de se focaliser sur les nombres eux-mêmes.
Les ACP et la construction du nombre
|
|
L’objectif principal du travail mathématique en CP est la construction du nombre. Ce travail est réparti tout au long de l’année : le nombre pour représenter une quantité, la numération de position, le calcul, le calcul mental, les opérations, sont autant d’apprentissages spécifiques qui nécessitent un travail étalé dans le temps, spiralaire et rigoureux. Ce n’est pas l’objet des ACP que de découvrir des nombres qui n’ont pas encore été étudiés en classe. Par exemple dans les 6 ACP du module 1 où l’objet est de travailler les transformations additives, les nombres en jeu ne dépassent jamais 10 et les calculs sont simples afin que les connaissances numériques nécessaires ne soient pas un obstacle à la compréhension des problèmes proposés. Cependant, c’est au travers de la résolution de problèmes et de son utilisation dans les problèmes que le nombre prend tout son sens : c’est cette stratégie pédagogique que nous proposons dans les ACP (voir les choix didactiques des ACP de CP). D’autre part, les élèves ne progressant pas tous à la même vitesse, la taille des nombres peut être une variable de différenciation. On proposera dans la plupart des ACP, suivant les groupes de besoins des élèves, des problèmes de structure identique mais avec des nombres en jeu plus ou moins grands. Enfin, pour entrainer et mesurer le degré d’acquisition des connaissances numériques de ses élèves, l’enseignant pourra tout au long de l’année, utiliser les Activités Entrainement Individualisé (ou AEI) du site Roma ou d’autres supports. |
Les ACP et le sens des opérations
|
|
C’est la résolution de problèmes qui donne leur signification à toutes les connaissances mathématiques et donc en particulier aux connaissances numériques comme les opérations élémentaires. Ainsi, les opérations sont introduites par la résolution de problèmes et les situations relevant de l’addition et de la soustraction sont travaillées de manière quasi simultanée ; il en est de même des situations relevant de la multiplication et de la division. En variant les situations, l’élève pourra dépasser ses conceptions premières et se détacher d’un focus trop exclusif sur les nombres en cherchant à reconnaitre une structure, c’est-à-dire un modèle, qui généralise les situations de type additif. Ce n’est qu’ultérieurement et progressivement que ce modèle sera transcrit avec des écritures mathématiques utilisant les signes + - et =. |
Les ACP et le calcul
|
|
Calculer c’est mettre en relation des quantités autrement que par une action physique sur les collections. Par exemple, additionner c’est passer progressivement de la réunion et au comptage des objets, à la récupération directe du résultat en mémoire en utilisant des règles de calcul : il y a donc toute une progression à suivre pour quitter petit à petit le recours aux collections en remplaçant les objets par des représentations numériques. Ce travail fait partie de la construction du nombre travaillée en classe dans toutes les activités mathématiques et autres. Les ateliers des ACP sont l’occasion pour les élèves de réinvestir ce qu’ils ont appris en classe sans pour autant constituer un obstacle supplémentaire dans la compréhension des énoncés : c’est pourquoi dans les ACP, les compétences en calcul se limiteront à celles que les élèves maitrisent par ailleurs. Cependant, au cours des séances d’ACP et de résolution de problèmes, il est essentiel d’inciter fortement les élèves à utiliser le calcul (principalement le calcul mental) plutôt que le comptage (et l’utilisation de la file numérique). |
Pour résumer, voici un tableau qui détaille les compétences numériques mobilisées dans l’ensemble des 5 modules du CP (à voir dans l'onglet bibliothèque).
Modules |
Compétences numériques mobilisées dans les modules |
| Module 1 |
Oral : compter ou calculer le résultat (réponse à la question) jusqu’à 10. Écrit : écrire les nombres jusqu’à 10. Calcul oral : connaitre toutes les sommes jusqu’à 10. |
| Module 2 |
Oral : donnaître les mots nombres entre 10 et 20. Ecrit : produire une égalité mathématique. Ex : Problème : Dans un sac, il y a 11 billes. Il y a 8 petites billes et des grosses billes. Combien y a-t-il de grosses billes dans le sac ? Réponse : 3 car 8 + 3 = 11 (justification) Calcul oral : connaitre toutes les sommes jusqu’à 20. |
| Module 3 |
Oral : connaître les mots nombres inférieurs ou égaux à 30. Ecrit : comprendre le sens des écritures mathématiques. Calcul oral : connaitre toutes les sommes jusqu’à 30. Calcul écrit : produire une égalité avec les signes+ ou – et des petits nombres. 6 + 3 = ? ou 2 + ? = 6 ou 6 - 2 = ? |
| Module 4 |
Oral : : connaître les mots nombres inférieurs ou égaux à 30. Écrit : écrire les nombres jusqu’à 15. Calcul : domparer 2 nombres inférieurs à 15 avec des écarts inférieurs ou égaux à 5. |
| Module 5 |
Oral : dénombrer une collection jusqu’à 30 compris. Écrit : décomposer les nombres inférieurs et égaux à 20. Calcul : connaitre toutes les sommes jusqu’à 30. Partager des quantités en 2 ou 3 ou 4 ou 5. |
La place des activités langagières dans les ACP de CP
L’expérimentation et donc en CP, la manipulation, sont essentielles pour favoriser la construction des concepts mathématiques, mais leur apprentissage et leur acquisition nécessitent un temps de représentation. En mathématiques, il existe plusieurs systèmes langagiers pour ce travail de représentation : le langage verbal (oral et écrit), les dessins, les schémas, les tableaux (plus tard les graphiques) et les symboles (chiffres, signes, codes). Dès le CP, il est fondamental d’aider les élèves à passer d’un registre à l’autre que ce soit pour dénombrer et coder les quantités, pour calculer ou pour comprendre une situation problème.
Au cours des séances d’ACP, tous ces registres sont sollicités chez les élèves :
- La verbalisation pour décrire une situation, en utilisant un langage précis et rigoureux : par exemple, distinguer et utiliser à bon escient des termes spécifiques (au début, à la fin, en tout, chaque, chacun, …), savoir poser une question et sur quoi elle porte …
- La verbalisation pour expliciter une démarche et se faire comprendre des autres dans les échanges en progressant doucement ainsi dans une posture métacognitive.
- La verbalisation pour argumenter un point de vue dans les débats entre pairs et aller petit à petit vers l’expression de son raisonnement.
- La schématisation en passant par l’expérimentation avec un matériel, puis par des dessins pour tendre lentement vers des représentations plus abstraites, des schémas et enfin des écritures symboliques.
- Le langage symbolique et mathématique, niveau d’abstraction qui permet un niveau de généralisation et de conceptualisation supérieur. En CP, un travail essentiel doit être fait autour de l’utilisation des signes opératoires et du signe égal.
Pour résumer, voici un tableau qui détaille les compétences langagières mobilisées dans l’ensemble des 5 modules du CP disponibles dans la bibliothèque.
Module 1 |
|
Module 2 |
|
Module 3 |
|
Module 4 |
|
Module 5 |
|
L’organisation des ateliers d’ACP dans la classe de mathématiques en CP
Les élèves sont répartis en petits groupes ou en ilots. Le groupe des élèves qui ne travaillent pas sur les ACP font un travail autonome (AEI ou toute autre activité proposée par l’enseignant) et les groupes sont ensuite échangés. Ces ateliers sont prévus pour être vécus par les élèves une fois par semaine. En CP chaque séance dure au maximum 45 minutes et peut être poursuivie ou reprise si besoin. L’utilisation du matériel est systématiquement proposée et organisée. Pour chaque atelier, il est proposé 2 parcours possibles en fonction des besoins des élèves :
- Un parcours * allégé pour les élèves les plus en difficultés en leur laissant ainsi plus de temps pour manipuler et s’approprier les situations.
- Un parcours ** pour les élèves les plus performants.
Des activités d’entrainement quotidiennes sont prévues et organisées entre chaque séance d’ACP à l’aide des banques de problèmes fournies dans la bibliothèque des ACP.
Le but des ateliers est de laisser le plus possible la parole aux élèves en favorisant les échanges entre pairs et non pas de leur apporter des réponses directement et souvent trop précocement. La place de l’oral joue un rôle prépondérant. Les échanges portent sur les hypothèses des élèves dans leur interprétation de la situation, sur leur validation ou non par le groupe en s’appuyant sur les données du problème et leurs relations. Le traitement de l’erreur a une place importante dans les échanges.
Déroulement d’un atelier d’ACP
Etape 1Appropriation des énoncés et de la consigne |
5 min environ |
Etape individuelle |
|
Etape 2Début d’interprétation par 2 ou en îlots |
15 min environ |
Etape orale collective |
Les élèves manipulent et commencent à faire des hypothèses de sens à plusieurs et à confronter leurs points de vue : attention, s’il leur est proposé une fiche-élève, ils ne la remplissent pas à cette étape ; ils travaillent sur ardoise ou papier de brouillon ou sur une affiche remplie en groupe. |
Etape 3Confrontation des diverses interprétation, échanges et débat |
15 min environ |
Etape orale collective |
L’enseignant recueille les différentes hypothèses des élèves (toutes les hypothèses sont acceptées oralement ou à partir de la présentation des affiches) et note :
|
Etape 4 |
5 min environ |
Etape individuelle |
Les élèves doivent se réapproprier la situation et résoudre le problème individuellement : si une fiche-élève a été donnée en début d’atelier, ils la remplissent à ce moment-là ou ils utilisent un autre support choisi par l’enseignant (cahier, feuille de classeur…). |
Etape d’entraînement |
10 min par jour |
Etape orale collective |
L’enseignant propose quotidiennement, au moins 2 problèmes à résoudre pour stabiliser ce qui a été appris au cours de l’atelier précédent. |
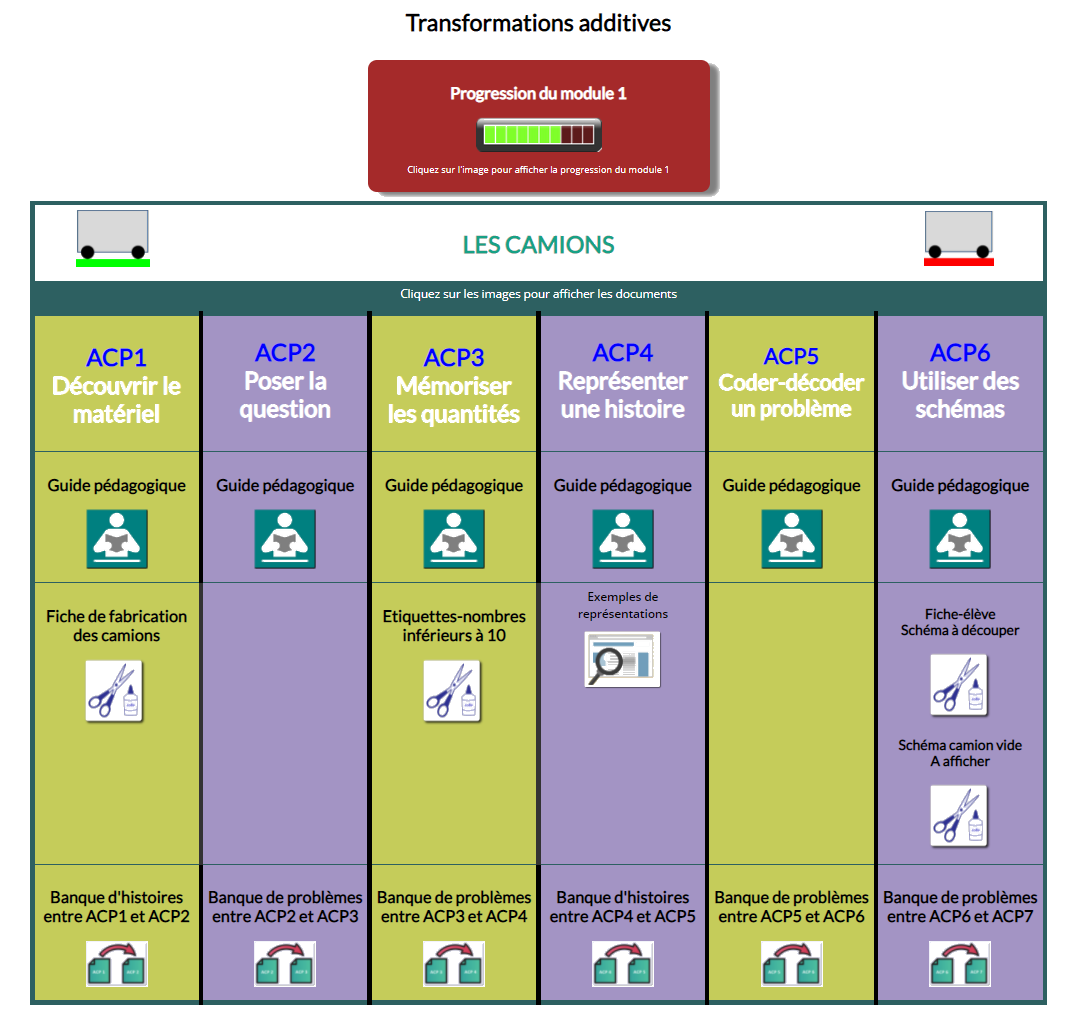
Au cours de l’année, les 26 séances d’ACP travaillées en CP sont réparties en 5 modules.
La progression des ACP de CP
 |
MODULE 1 : TRANSFORMATIONS (matériel les camions) |
|
ACP1-camions1 : découvrir les transformations avec le matériel des camions ACP2-camions2 : rechercher l’état final en posant la question : à la fin, combien ? ACP3-camions3 : rechercher l’état final en mémorisant les quantités ACP4-camions4 : représenter une situation d’ajout ou de retrait ACP5-camions5 : coder et décoder un problème ACP6-camions6 : utiliser des schémas |
|
 |
MODULE 2 : COMPOSITIONS (matériel les ânes) |
|
ACP7-ânes1 : découvrir les compositions avec le matériel des ânes ACP8-ânes2 : catégoriser avec recherche du tout ACP9-ânes3 : représenter un problème avec recherche du tout ACP10-ânes4 : représenter un problème avec recherche d’une partie ACP11-ânes5 : rechercher le tout ou une partie ACP12-ânes6 : utiliser des schémas |
|
 |
MODULE 3 : APPROFONDISSEMENT : problèmes mixtes de compositions ou de transformations (matériel les camions et les ânes) |
|
ACP13-mixte1 : modéliser - passer d’un énoncé à un schéma ACP14-mixte2 : modéliser -passer d’un énoncé à une écriture mathématique ACP15-mixte3 : modéliser --identifier transformations et compositions dans des contextes variés ACP16-mixte4 : modéliser- traduire un schéma par un énoncé verbal ACP17-mixte5 : modéliser-passer d’une écriture mathématique à un énoncé verbal |
|
 |
MODULE 4 : COMPARAISONS ADDITIVES (matériel les immeubles) |
|
ACP18-immeubles1 : découvrir les comparaisons additives positives avec le matériel des immeubles ACP19-immeubles2 : utiliser les expressions de plus (moins) que et leur réversibilité ACP20-immeubles3 : associer des problèmes de comparaisons additives à des dessins d’immeubles ACP21-immeubles4 : utiliser des schémas ACP22-immeubles5 : Résoudre des problèmes de comparaison additive dans des contextes variés |
|
 |
MODULE 5 : PARTAGES ET GROUPEMENTS (matériel les pirates) |
|
ACP23-pirates 1 : Résoudre des situations de partage avec le matériel des pirates ACP24-pirates 2 : Résoudre des situations de partage dans des contextes variés ACP25-pirates 3 : Résoudre des situations de groupements avec le matériel des pirates ACP26-pirates 4 : Résoudre des situations de partage et de groupements dans des contextes variés. |
|